카오스 제어 (86) - 진동하는 MEMS에서 비선형 동력학(5)
배영철 전남대학교 공과대학 전기공학과 교수(ycbae@chonnam.ac.kr)
이번 호에서는 진동하는 MEMS에서의 비선형 동력학에 대한 연구 마지막 내용으로서 비선형 확률 공진에 기반을 둔 진동을 이용한 에너지 하비스팅과 MEMS 열탄성 제동상의 기하학적 비선형성 효과를 중심으로 설명한다.
C.R. McInnes, D.G. Gorman, M.P. Cartmell 연구
C.R. McInnesa, D.G. Gormana, M.P. Cartmell[1]은 2008년 Journal of Sound and Vibration에 발표한 “Enhanced vibrational energy harvesting using nonlinear stochastic resonance(비선형 확률 공진을 이용한 개 선된 진동 에너지 하비스팅)”이란 제목의 논문을 통하여 수직 적으로 여기된 에너지 하바스팅 기구에 주기적 강제 항을 인 가함에 의해 소자로부터 유용한 전력은 주기적 강제 힘없이 기구에 대하여 명확하게 개선되었음을 증명했다. 또한 이 논문에서는 새로운 효과를 검증하기 위하여 개념 적으로 간단하지만 이와 같은 소자가 실제로 가능한 모델을 진동 에너지 하비스팅을 개선하기 위하여 확률적 공진의 사 용을 위한 연구 결과를 제시했다.
1. 에너지 하비스트 기구
1) 클램프-클램프 빔의 자유 진동
진동 에너지 하비스팅에서 확률 공진의 응용을 탐구하기 위하여 개념적으로 간단한 기구를 연구했다. 여기서는 적당한 압축 부하가 2개의 대칭 평형 상태들의 하나 속으로 채워질 수 있는 빔을 고려했다. 이 빔은 무시할 수 있는 질량의 기반 위에 지지된다. 빔의 필수적인 거동은 그림 1에서 보여주는 것과 같이 강체 k와 자연 길이 l의 2개 선형 스프링을 가진 단일 집중 질량으로서 거동을 표현함으로 잡을 수 있다.
빔에서의 변위는 단일 선형 제동기 c에 의해 모델링 될 수있다. 이러한 집중 질량 모델을 이용한 질량의 변위는 A-A´의 기준 ![]() 으로부터 x에 의해 정의되며 한편 스프링은 2d 즉, d
으로부터 x에 의해 정의되며 한편 스프링은 2d 즉, d
여기서 식(1)에서의 새로운 비선형 항은 스프링-질량 시스템을 나타낸다. 이 비선형 항은 x/d≪1의 가정에 의해 확장될 수 있다. 이러한 제한이 나중에 사용되지 않을지라도 운동의 결과 방정식은 문제의 완전한 비선형성을 나타내며 이것은 식(2)와 같이 표시한다.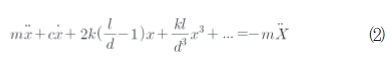
 정의될 수 있다. 따라서 빔에 대한 정량적 비선형 모델은 식 (3)과 같이 정의된다.
정의될 수 있다. 따라서 빔에 대한 정량적 비선형 모델은 식 (3)과 같이 정의된다.
여기서 ·는 τ에 대응하는 미분을 나타낸다.자유 파라미터 μ=2(l/d-1)은 빔상의 압축 부하의 측정으로서 사용되며, ![]()
![]() 가진 비제동, 비여자 시스템을 먼저 고려하자. 명확하게 만약 빔이 장력 l< d 속에 있으면 μ< 0이고, 반면 만약 빔이 압축 l > d에 있으면 μ=0에 대응하여 임계버클링 부하를 가진 μ>0이 된다. 이것은 μ< 0에 대하여 볼 수 있다.
가진 비제동, 비여자 시스템을 먼저 고려하자. 명확하게 만약 빔이 장력 l< d 속에 있으면 μ< 0이고, 반면 만약 빔이 압축 l > d에 있으면 μ=0에 대응하여 임계버클링 부하를 가진 μ>0이 된다. 이것은 μ< 0에 대하여 볼 수 있다.
식(3)은 장력에서 편향되지 않는 빔에 대하여![]()
![]()
![]()
그런 후 초임계 분기가 μ의 부호가 변화할 때 발생한다[3].위에서 설명한 시스템의 정량적인 거동 변화는 ![]() 와 같은 문제 V(ζ)에 대한 효과적인 퍼텐셜의 사용을 통해 보여왔다. 퍼텐셜은 식(4)와 같이 정의될 수 있다.
와 같은 문제 V(ζ)에 대한 효과적인 퍼텐셜의 사용을 통해 보여왔다. 퍼텐셜은 식(4)와 같이 정의될 수 있다.
위에서 정의한 평형점들의 안정성 특성들은 그림 2에서 보여주는 것과 같이 V(ζ)의 전환점들로부터 결정될 수 있다.








2) 클램프-클램프 빔의 강제 진동
클램프-클램프 빔의 간단한 모델은 위에서 논의한 선형 제동 항과 여기를 포함하여 확장하게 될 것이다. 파라미터 μ는 주파수 ω와 진폭 η에서 강제할 수 있다. 이것은 거리 A-A´가 현재 시간에 따라 변화하게 하려고 발진적인 방법에서 압축과 완화되고 있음을 함축한다.
이와 같은 힘은 그림 1에서 나타낸 것 같이 지지 점 A와 A´에서 전자기계적 액추에이터를 가지고 달성될 수 있다. 이 강제 힘은 확률적 공진을 허용하도록 퍼텐셜 장벽의 높이를 조절하게 될 것이다. 이것은 또한 빔이 외부 잡음 Q(t)에 의해 여기된다고 가정될 수 있으며 이 특성은 나중에 설명한다. 기구의 동력학들은 파라메트릭하게 강제되고 식(5)에 의해 정의된다.
이것은 선형 제동c –·ζ에 의해 소산된 여기 Q(t)로부터 메커니즘의 입력 에너지가 존재한다는 것을 알 수 있다.
중요하게 여기로부터 응답 빔까지 에너지의 이 흐름은 주파수 ω[4]에서 빔의 파라메트릭 강제에 의해 변조된다[4]. 문제의 유효 퍼텐셜은 시간 독립으로서 정의될 수 있으며 발진함수는 식(6)과 같이 주어진다.
퍼텐셜의 강제적인 힘은 반 사이클에 대하여 그림 3에 나타내었다. 이것은 시스템의 안정한 2개 평형점 사이의 퍼텐셜 장벽의 높이는 변조됐음을 볼 수 있다. 강제 주파수 ω를 통하여 적절하게 회전할 때 이 변조는 확률 공진에서 2개의 퍼텐셜 우물 사이의 메커니즘을 구동하기 위하여 Q(t) 여기를 허용하게 됨을 보게 될 것이다.
그런 후 빔에서 현저하게 개선된 응답은 에너지 하비스팅을 위해 탐험되고 제동됨으로 소산되는 더 큰 전력을 제공하게 될 것이다.

2. 개선된 진동 에너지 하비스팅
진동 에너지 하비스팅을 위한 확률 공진의 사용을 평가하기 위하여 댐퍼에 의해 소산된 전체 전력을 조사했다. 원리에서 이 전력은 에너지 하비스팅을 위해 유용하다. 댐퍼가 전기기계적 소자[5] 또는 압전 스트립[6](연속 빔을 나타내는 스프링-질량 시스템)을 나나낼지라도 댐퍼의 상세성은 고려하지 않았다. 주파수 ω에서 빔의 빌잔 강제를 구동하기 위해 전력이 요구된다는 사실에 주목한다.
이것은 전체 유용한 전력으로부터 추출될 것이다. 전통적인 확률 공진은 주기 신호에 잡음을 추가했으나 이 설명의 시스템은 확률적으로 여기한 후 주기적인 힘을 가하였다. 식(5)는 식(7)과 같이 됨을 알 수 있다.
식(7)은 식(8)과 같이 다시 정리된다.
식(8)은 전력 보존의 항이 명확하다[5]. 우리는 선형 소산,메커니즘의 퍼텐셜 에너지와 운동 에너지의 변화율에 의해 평형되어진 여기 Q(t)로 인한 순간 전력 입력 사이의 평형으로서 식(8)을 해석한다. 따라서 ![]() 시스템의 전체 에너지를 식별하며 여기서 퍼텐셜 에너지의 유효성은 식(4)에 의해 정의되고 식(9)와 같이 정리된다.
시스템의 전체 에너지를 식별하며 여기서 퍼텐셜 에너지의 유효성은 식(4)에 의해 정의되고 식(9)와 같이 정리된다.
식(9)로부터 에너지 하비스팅에 대한 유용한 순시 전력 P를 식(10)과 같이 제안했다.
![]() 형 소산이다. 이것은 댐퍼가 빔에 부착됨으로 얻어지도록 가
형 소산이다. 이것은 댐퍼가 빔에 부착됨으로 얻어지도록 가
정된다. 여기서 주파수 ω에서 빔에 강제되어 수행한 일의 비율을 의미하는 2차 ![]()
그러나 이 항은 빔이 완화됐을 때 에너지를 제거하며 빔이 압축될 때 에너지 입력에 대응하는 부호가 될 수 있다. 생성된 전체 전력의 보존 추정을 제공하기 위하여 이 항은 오직 에너지의 하강을 보장하며 따라서 식(11)과 같이 정의된다.
따라서 에너지 하비스팅에 대하여 유용한 전력은 주파수 ω에서 전력이 빔에서 힘을 가하는 것을 요구하기 때문에 줄여들게 된다.
확률 공진을 시뮬레이션하기 위하여 여기 Q(t)를 정의한다. 순수한 백색 잡음 대신에 많은 고조파 수들은 합쳐지고 강한 백색 잡음 성분은 추가된다. 고조파들은 각 속도 ω와 클랭크 길이 con-rod 길이 비율 1/3을 가지고[7] 회전하는 단일 실린더 엔진으로부터 방사된 에너지를 표현하도록 가정했다. 그런 후 백색 잡음은 여기가 식(12)와 같이 정의되도록 하기 위하여 엔진의 비모델링된 고주파 동력학을 나타내기 위하여 이 주기 신호에 추가했다.
여기서 백색 잡음 ρ(t)는 영 평균값을 가지며 단위 분산과 계수들은 주기 진동 스펙트럼[7]에서 근사를 나타낸다.
여기서 빔의 주기적인 힘의 유무를 가지고 메커니즘의 응답을 고려했다. 이들 자연 길이의 약 65%에 압축된 스프링 상태에 대응한 후 주파수 ω를 가지고 거리 A-A´가 근사적으로 15%에 의해 변조하는 값인 μ=1, η=0.7을 선택했다.
0의 힘(η=0)를 가지고 메커니즘은 그림 4에서 보여주는 것과 같이 작은 진폭 진동을 가지고 단일 퍼텐셜 우물에서 여기된다.
그러나 주기적인 힘(η=0)을 가지고 메커니즘은 그림 4에서 다시 보여준 큰 진폭 변위들을 가지고 확률 공진 상태에서 2개의 퍼텐셜 우물 사이에서 섭동한다. 확률 공진에서 메커니즘은 선형 소산 ![]() 증진된 것과 같이 크게 여기된다. 그러나 식(10)에서 추가적인 항은 일이 빔의 강제적인 힘에서 수행하기 때문에 출력에서 이 증가는 감소하게 될 것이다. 2가지 경우로부터 전체 통합된 에너지 출력은 그림 4에서 보여주고 있다.
증진된 것과 같이 크게 여기된다. 그러나 식(10)에서 추가적인 항은 일이 빔의 강제적인 힘에서 수행하기 때문에 출력에서 이 증가는 감소하게 될 것이다. 2가지 경우로부터 전체 통합된 에너지 출력은 그림 4에서 보여주고 있다.
확률 공진에서 강제적으로 힘을 가한 메커니즘은 강제하지 않은 메커니즘보다 여기 Q(t)로부터 더욱 현저하게 많은 에너지를 명확하게 수송하고 있음을 볼 수 있다. 확률 공진에 대해 요구된 강제 주파수 ω는 퍼텐셜 우물[8] 사이의 천이 확률인 Kramer's 비율로부터 추정할 수 있다.
확률 공진으로부터 멀어진 메커니즘의 응답을 그림 5에 보여주고 있다. 이 경우에 메커니즘은 2개의 퍼텐셜 우물 사이에서 불안정한 천이이다. 통합된 에너지 출력은 빔에 강제적인 힘을 가한 작업 수행으로 인하여 힘을 가하지 않은 기구에 대하여 더 큼을 볼 수 있다. 마지막으로 강제적인 힘 메커니즘과 비강제적인 메커니즘으로부터 유용한 전력은 그림 6에 보여주고 있다.
그림 6으로부터 강제된 메커니즘이 강제되지 않은 메커니즘보다 현저하게 더 많은 힘을 소산함을 알 수 있으나, 이들전력의 몇몇은 빔에 힘을 주는 것을 요구한다. 그러나 전체 유용한 전력과 통합된 에너지 출력은 확률 공진에서 보다 크다. 진동 에너지 하비스팅에서 확률 공진의 소개된 응용을 가지고 이것은 다른 기계적 시스템들이 이 현상의 존재 가능성을 보여주고 있음이 명백하다
C. Mendez, S. Paquay, I. Klapk J.-P. Raskin[9] 등의 연구
C. Mendez, S. Paquay, I. Klapk, J.-P. Raskin 등은 2009년 Nonlinear Analysis: Real World Applications에
발표한 논문“Effect of geometrical nonlinearity on MEMS thermoelastic damping(MEMS 열탄성 제동상의
기하학적 비선형성 효과”란 제목의 논문을 통하여 캔틸레버빔의 간단한 MEMS 구조에 대한 수치 시뮬레이션으로 기하학적 비선형 효과들이 열탄성 제동을 포함한 시뮬레이션에서 고려되었을 때 선형 근사의 결과가 어떻게 나타나는지를 보여주었다.
이 분석은 변위가 클 때 시스템의 경화(주파수 증가)와 발진 진폭에 대한 붕괴 시간의 증가를 보여주고 있다. 이들 사실의 고려는 높은 품질 MEMS 공진기의 설계 개선을 위해 유용하며 여기서 이들 관계를 설명한다.
1. 매크로 크기와 마이크로 크기에서 열탄성 결합
기계적과 열적 영역 사이의 상호작용을 고려할 때 기계적 방정식에서 열효과를 포함해야만 한다. 잘 알려진 열팽창 효과는 식(13)과 같이 주어지는 변형 ε에 대한 구성적인 관계에 서 추가적인 항을 통하여 모델링 된다[10].
여기서 σ는 응력, S는 순응 텐서, α는 열팽창 계수의 텐서,θ는 주변 절대 온도 T0에서의 상대적인 온도이다.
한편, 열평형 방정식에서 식(13)은 시스템 상에서 수행될수 있는 기계적 작업을 계산해야만 한다. 엔트로피 S의 정의로부터 식(14)가 유도된다.
여기서 T는 절대 온도, dQ는 시스템에 부가된 열의 양이다. 단위 체적 η=dS/dV당 엔트로피의 시간 전개는 식(15)와 같이 주어진다.
여기서 q는 열자속 벡터이다.
만약 기계적 작업이 없는 것을 고려한다면 이 표현은 식 (16)과 같은 잘 알려진 열방정식을 유도한다.
Cv는 일정한 체적에서 단위 체적당 열 용량을 나타낸다. 만약 지금 기계적 작업으로 인하여 엔트로피가 변화할 수 있다는 것을 고려한다면 열동력 관계를 이용하고 독립 변수로 서 변형과 온도를 고려하면 식(17)과 같이 정리할 수 있다[10].
여기서 C=S-1은 강성 텐서이다. 따라서 열 Qth-el의 추가적인 열탄성은 식(18)과 같이 주어진다.
식(18)은 식(16)의 우변 항을 포함해야 한다. 일반적으로 절대온도 T는 열적 원점의 비선형성을 회피하기 위하여 주변 절대온도 T0에 의해 변경된다. 식(18)과 식(13)에서 αθ항들은 기계적 열적 방정식 사이의 결합 항이다. 변형은 변위의 함수이며 따라서 식(13) 때문에 온도에 의존한다. 덧붙여 온도는 변위의 시간 미분 즉, 식(18)으로 인하여 속도에 의존한다. 따라서 열적 결합을 고려함에 의해 속도에 비례하는 항은 변위 방정식에서 나타나며 이것은 제동원이다.
이상의 설명은 방정식의 유한 요소 이산화된 형태에서 더 잘 볼 수 있다. 노달(nodal) 변위와 상대적 온도를 각각 U와 θ로서 고려하면 해를 가진 대수 시스템은 식(19)와 같이 정리된다[11].
여기서 MUU는 질량, DUU는 점성 제동, DUθ는 열탄성 제동,Dθθ는 열용량, KUU는 강성, KUθ는 영팽창, Kθθ는 열전도성,Fext는 힘, Qext는 열원이다.
이 방정식에서 파라미터 θ의 해가 구해짐을 볼 수 있으며 U · 의 열탄성 제동 서브행렬을 가진 곱이기 때문에 이것은U ·의 속도에 의존한다. 따라서 온도가 열적 서브행렬 KUθ에 곱해질 때 이것은U ·를 포함하는 항을 가진 변위에 대하여 공헌하게 될 것이며, 이 항은 점성 제동DUU가 0일 때조차도 기계적 제동을 생성하게 될 것이다.
대부분 경우에 시스템이 마이크로스코프일 때 열탄성 제동은 점성 제동보다 훨씬 덜 중요하므로 이것은 항상 거의 무시한다. 그러나 점성 제동이 최소화될 때 진공에서 MEMS 공진기와 같이 마이크로스코픽 시스템을 고려했으며 언제나 존재하는 열탄성 제동은 이들 소자들의Q인자를 제한하는 주요원인이 될 수 있다[12].
Q인자 계산을 위한 연구 결과[13]에서 제너(Zener) 표현은매우 우수한 근사값을 가지며 매크로와 마이크로 시스템의 경우에 옅탄성 제동의 영향을 비교할 수 있다. 이러한 계산을 수행하기 위하여 식(20)과 같이 작은 차원이 없는 파라미터 △E를 정의하는 것이 편리하다.
여기서 주변 절대온도 T0와 열팽창 계수 α를 제외하고 이것은 거의 일정 압력 Cp에서 단위 체적당 열 용량과 영률(Young's) 모듈로 나타난다. 차수 △2E 의 보정을 무시하면 빔에 대한Q인자의 역은 식(21)과 같이 주어진다.
0에서부터 무한대의 범위를 가지는 차원이 없는 변수 ξ는 식(22)와 같이 정의된다.
여기서 k는 열전도도, h는 빔의 높이, ω 는 등열 고유주파수이다. 빔 고유 주파수들은 식(23)과 같이 주어진다.
여기서 L은 길이, ρ는 밀도, an은 빔과 고려된 모드의 경계 조건에 의존하는 계수들이다. 예를 들면 클램프드-클램프드빔에 대하여 처음 3개 모드들에 대한 an 계수들은 an=(4.730,7.853, 10.996)이다. 따라서 식(22)와 식(23)으로부터 식(24)와 같이 정리할 수 있다.
식(21)의 함수 f(ξ)는 ξ≅2.225에서 최대의 값을 가지며 △E는 오직 재료 특성에 의존하며, 예를 들어 실리콘 빔의 최소 Q 인자는 Q≅9790이다. 이는 표 1의 실리콘 특성을 사용하여 얻은 것이다.
클램프-클램프 빔의 기본 모드 비교는 즉, a0=4.73,L/h=10을 취하면 최소 Q 인자는 h≅8㎛에 대응한다. 그러나
동일 L/h=10을 유지하고 h=8cm(ξ≅222.5)을 취하면 Q≅4×107과 동일한 것으로 대체한다.
이것은 매크로스코픽 시스템에서 열탄성 제동이 거의 항상 무시하는 이유이며 거의 모든 경우에 Q 인자가 보다 낮은 점성 제동에 의해 제한되기 때문이다. 그럼에도 불구하고 점성 제동이 최소화될 때 MEMS 발진기들은 차수 1×104의 Q 인자를 달성할 수 있으며 따라서 열탄성 제동은 MEMS에서 Q 인자를 제한할 수 있는 원래부터의 효과로서 고려해야만 한다.
2. 자유 발진들의 과도 동적 시뮬레이션
Q 인자를 계산하는 것과 제동을 추정하기 위한 하나의 방법은 빔에 대하여 자유 발진의 과도 시뮬레이션을 만드는 것이다. 이것은 앞에서 설명한 방정식에서 이미 포함되어 있으며Q 인자는 동일한 진폭에서 계산되어 진다. 여기서는 이 한계에서 유용한 시뮬레이션 결과를 제시하고 큰 변위에 대하여 유용한 비선형 시뮬레이션의 결과를 가지고 비교한다.
선형과 비선형 결과들 사이의 차이를 보다 시각화하기 위하여 사례로서 캔틸레버 빔을 적용한다.
덧붙여 제동의 효과를 보기 위한 필요한 발진 수를 최소화하기 위하여 빔의 기하학과 차원들은 Q 인자가 거의 최소인것과 같다. 따라서, 여기서는 1.25mm 높이와 125mm 길이를 가진 실리콘 캔틸레버 빔의 과도 시뮬레이션을 수행했다.
이것은 Q 인자가 Q≅1.2×104과 같은 값으로 주어지지만, 이 Q 인자가 거의 실리콘 빔에 대하여 최소일지라도 이것은 진폭에서 붕괴값을 보는 것을 원하는 과도 시뮬레이션에 대하여 아직까지 높은 값이다.이러한 이유로 식(20)에서 인자 100을 곱하여 정의한 △E파라미터의 제동 곱을 인공적으로 증가시켰다. 이 방법에서 파라미터 △E는 작은 값(△E ≅0.02)으로 남아있지만, Q 인자는 Q≅120이 되며 2개의 붕괴 시간을 포함한 시뮬레이션은
적절한 계산 시간 내에서 수행될 수 있다.
3. 선형 근사 결과
변위가 작을 때 선형 근사는 매우 우수한 결과들을 보여주며 그 구현의 단순성 이외에 이것은 계산의 많은 시간을 요구하지 않으므로 수치 시뮬레이션에서 선호한다. 근사는 변위u에서 다음과 같은 선형 표현의 식(13)과 식(18)의 텐서 변형ε에 대하여 식(25)와 같이 정리된다.
여기서 x는 초기 배열의 좌표이다.
시뮬레이션한 시스템은 제동 자원이 오직 열탄성 계수인 앞서 기술한 실리콘 캔틸레버 빔이다. 그림 7에서 시간의 함수로서 빔 팁의 변위를 볼 수 있다.
그림 7에서 보여주는 데이터를 이용하여 FFT(Fast Fourier Transform)을 만들 수 있으며 발진의 기본 주파수
ω를 얻을 수 있다. 그림 8에서 빔 진동의 기본 모드에 대응하여 ωFFT≅2π112.3rad/s≅705.6rad/s에서 중심을 가진 잘 정의된 최대 값이 주어짐을 알 수 있다.
시간 지연 τ를 얻기 위해 자연 알고리즘 크기의 그림 6에서 곡선의 절대값의 최대를 그릴 수 있다. 그림 9에서 보여주는 최대는 τlin_ fit ≅1/3.036s≅0.33s 값에서 주어진 직선에 의해 매우 적합하게 되었다.
Q 인자의 정의를 이용하여 시뮬레이션으로부터 얻어진 위에서의 2개의 값들은 주어진 Q~ul=ωFFTτlin_ fit/2≅116 값으로 조합될 수 있다. 이 값은 해석적인 하나의 값으로 매우 잘 비교된다. Qanalyt≅120은 식(21)로부터 계산했다.
4. 비선형 결과
시스템에서 큰 변위가 발생했을 때 식(25)에서 주어진 변형에 대한 선형 근사는 더 이상 유용하지 않다. 대신 식(26)에 의해 주어진 비선형 Green-Lagrange를 고려해야만 한다.
이에 대한 구현이 보다 어렵고 시간들이 더 길지라도 만약 큰 변위가 주어질 때 비물리적인 결과를 얻기 원하지 않는다면 변형의 사용은 필수적이다. 예를 들어 자유 발진 동안의 빔의 변형을 그림 10에 보여주고 있다.
선형 근사는 변형이 클 때 변위들의 우수한 설명을 제공하지 못함을 볼 수 있다. 선형 결과의 일반적인 특성들은 축 빔 방향에서 실제적인 변위들을 가지지 못한다. 기하학적 비선형을 고려했을 때 빔 팁의 변위를 그림 11에 제시했다.
식(25)에 의해 정의한 극미세 변형 대신에 사용된 식(26)에 의해 주어진 Green-Lagrange 변형이 있을 때 응력과 변위 사이의 관계는 수정된다. 결론적으로 시스템 강성은 변화되고, 이 사실은 이것의 고유 모드들의 주파수 값에 반영되어야만 한다. 그림 12는 그림 11의 비선형 데이터의 FFT 분석 결과이다.
선형 경우와 같이 잘 정의된 최대는 아니며 곡선의 형태는 보다 복잡하다. 실제로 이 형상은 발진 진폭을 가진 주파수의 변화보다 더 반영하는 것은 없다.
다른 시간에서 FFT 해석을 검증하기 위하여 그림 13을 제시한다. 진폭이 클 때 비선형 시뮬레이션은 구조의 경화성을 나타내는 선형 예측과 비교하여 더 높은 주파수를 제공한다. 진폭이 줄어들 때 비선형 결과들은 예측된 결과로서 선형의 것과 동일하게 된다. 비선형 Green-Lagrange 변형이 사용될 때 시스템의 강성은 수정된다. 식(18)에서 볼 수 있는 것과 같이 이것의 시간 미분을 통하여 변형은 또한 열탄성 제동의 기원이 되는 결합항의 일부분을 취한다. 따라서 큰 변위가 발생할 때 제동에서의 수정이 예상된다.
그림 14에서 그림 9와 등가인 비선형의 경우를 보여준다. 비선형의 경우에 빔 팁의 발진 진폭은 시간의 일정한 붕괴와 함께 줄어들지 않는다는 것을 보여준다. 우리가 예상한 것과 같이 변위가 커지고 작은 변위에서 선형 값이 복원될 때 진폭에 대한 붕괴 시간은 곡선 기울기와 역으로 증가한다.
비선형 거동에서 이러한 거동에 대하여 2개의 가능성이 있는 이유가 존재한다. 첫째 앞서 언급한 것처럼 제동 자체에서 비선형성을 소개할 수 있다는 것이며, 둘째 이들 결과들이 그림 10에서 보여주는 것과 같이 비선형의 경우에 빔 형상이 보다 우수하다는 설명이 될 수 있다는 것이다.
두 번째의 경우에 진폭에 대한 붕괴 시간에서 변화에 대한 이유는 보다 위상학적 원점을 가진다는 것이며 실제 경우에 있어서 빔 팁의 변위는 선형 근사에 의해 예측된 것만큼 클 수가 없다는 것이다.
그림 15에 선형과 비선형 시뮬레이션에 대한 운동 에너지의 최대를 제시했다. 비선형 경우에 대한 경향이 그림 14에서와 같을지라도 결과들은 덜 결론적이다. 이것은 그림 10을 보면 쉽게 이해할 수 있다. 빔 팁의 비선형 경우가 선형보다 작을 동안 클램프 부근의 곡면 부근은 탄성 에너지의 더 큰 집중이 있음을 높게 나타낸다. 이것이 전체 빔의 에너지를 고려하는 이유이며 에너지에 대한 붕괴시간의 변화는 그렇게 명확하지 않다.
[참고문헌]
1. C.R. McInnesa,, D.G. Gormana, M.P. Cartmell, “Enhanced vibrational energy harvesting using nonlinear stochastic resonance”, Journal of Sound and Vibration, 318,pp. 655-662, 2008.
2. S. Roundy, P.K. Wright, J. Rabaey, “A study of low level vibrations as a power source for wireless sensor nodes”, Computer Communications 26 (11), pp.1131 1144,2003.
3. C.R. McInnes, T.J. Waters, “Reconfiguring smart structures using phase space connections”, Smart Materialsand Structures 17(2), 025030, 2008.
4. M.P. Cartmell, An Introduction to Linear, Parametric and Nonlinear Vibration, Chapman & Hall, London, 1990.
5. N.G. Stephen, “On energy harvesting from ambient vibration”, Journal of Sound and Vibration 293 (1 2), pp.409 425, 2006.
6. S. Roundy, P.K. Wright, “A piezoelectric vibration based generator for wireless electronics”, Smart Materials and Structures 13(5), pp.1131 1142, 2004.
7. D. Gorman, W. Kennedy, Applied Solid Dynamics,Butterworth-Heinemann, London, 1988.
8. T. Wellens, V. Shatokhin, A. Buchleitner, Stochastic resonance, Reports on Progress in Physics 67(1), pp.45 105,2004.
9. C. Mendez, S. Paquay, I. Klapk, J.-P. Raskin,“ Effect of geometrical nonlinearity on MEMS thermoelastic damping”, Nonlinear Analysis: Real World Applications, 10, pp.1579-1588, 2009.
10 A.N. Norris, D.M. Photiadis,“ Thermoelastic relaxation in elastic structures, with applications to thin plates”, Q. J. Mech. Appl. Math. 58, pp 143, 2005.
11. M. Sunar, S.S. Rao, Thermopiezoelectric control design and actuator placement, AIAA J. 35, pp.534, 1997.
12. A. Duwel, M. Weinstein, J. Gorman, J. Borenstein, P. Ward,“ Quality factors of MEMS gyros and the role of thermoelastic
damping”, in: Proc. Fifteenth IEEE International Conference on Micro Electro Mechanical Systems, vol. 214,2002.
13. R. Lifshitz, M.L. Roukes, “Thermoelastic damping in micro- and nano-mechanical systems”, Phys. Rev. B 61, pp
5600, 2000.