전 호에서는 수송체 시스템으로 사용되는 한 바퀴 구동 이동로봇 시스템의 제어와 응용을 다루었다. 이번 글에서는 최근 인기가 있는 무인비행체 중에서 쿼드로터 시스템에 대해 다루고자 한다. 무인비행체 관련해서 개인의 사생활 문제가 이슈화되고는 있지만, 지속적인 관심과 실용화로 그 영역이 확장되고 있다.
무인 비행체 시스템
최근 북한에서 넘어온 무인비행체가 연이어 발견되면서 우리 안보에 대한 걱정과 함께 무인비행체에 대한 관심이 커지고 있다.
무인비행체는 이착륙 구조에 따라 크게 두 가지 형태로 나눈다. 북한에서 넘어온 것과 같은 형태를 CTOL(Conven-tional Take-off and Landing) 구조라 하고 주로 장거리 비행에 사용한다. 반면 제자리에서 이착륙이 가능한 구조를 VTOL(Vertical Take-off and Landing) 구조라 하고 장거리보다는 단거리용으로 사용한다.
로터의 위치에 따라 움직이는 방향이 결정되므로 그림 1(a)은 CTOL 구조의 미국공군의 무인비행기 Predator이고 그림 1(b)는 VTOL 구조의 로터가 6개인 Hexarotor이다.
그림 1. 무인 비행체의 구조
미국 펜실베이니아 대학에서는 실내에서 여러 대의 쿼드로터들이 좁은 구멍을 통과하거나 편대 비행을 하는 등의 고난도 비행제어를 실험으로 검증했다[1]. 스위스의 ETH에서는 쿼드로터 시스템으로 탑을 쌓거나 탁구를 하거나 역진자를 제어하는 등 고난도의 자세제어를 실험으로 보였다[2]. 이처럼 고난도의 자세제어가 가능한 것은 실내에서 쿼드로터의 정확한 위치를 측정할 수 있었기 때문이다.
하지만 쿼드로터의 궁극적인 목적은 실외에서의 작업을 수행하는 것이다. 최근에는 민간용으로 다양한 분야에서 사용되고 있다. 예컨대, 공중에서 가까이 촬영하는 방송이나 영화, 고속도로의 사고 모니터링, 그리고 주변 감시를 통한 경호용 등으로 사용되고 있다. 이러한 작업을 성공적으로 수행하기 위해서는 호버링제어, 즉 자세제어가 중요하다.
학계에서는 이러한 자세제어에 대한 연구가 활발하게 진행되고 있다[3-12]. 신경회로망 제어기를 사용하기도 하고[7], 외란 관측기를 사용하며[8, 9], 시간지연 제어 방식을 이용하여 제어한다[10-12]. 대부분 제어방식은 외란에 대처하여 자세제어의 성능을 좋게 하는 것이 목적이다. 최근에는 영상을 이용한 위치제어를 하고[13], 사람과 협조제어를 하기도 한다[14].
이 글에서는 쿼드로터 시스템의 기구학과 동역학을 유도하고, 자세제어를 실험을 통해 검증해 보고자 한다. 제어방식으로는 선형제어 방식과 시간지연 제어 방식을 사용하여 그 성능을 비교해 보고자 한다.
쿼드로터 시스템 모델링
1. 좌표와 기구학
쿼드로터는 4개의 로터로 구성되어 있으며, 서로 반대방향으로 회전하는 두 쌍의 프로펠러를 가지고 있는 시스템이다.
그림 2의 4개의 로터에서 나오는 추력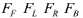 
을 이용하여 병진운동 
과 회전운동 
의 6자유도로 움직이는 under-actuated 시스템이다.
그림 2. 쿼드로터 시스템의 좌표계
속도는 다음과 같이 정의된다.
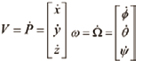(1)
글로벌 좌표에서 선속도와 각속도는 식 (1)과 같이 나타낼 수 있는데, 쿼드로터의 움직임을 나타내기 위해서는 식 (3)에서 식 (2)를 이용하여 글로벌 좌표에서 물체 좌표계로 좌표변환 해야 한다.
(2)
여기서 sø=sinø, sθ=sinθ, sψ=sinψ, cø=cosø, cθ=cosθ, cψ=cosψ으로 간략화해서 나타내었다.
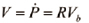(3)
식 (2)와 식(3)을 이용해서 계산한 물체 좌표계에서의 선속도, Vb는 식 (4)와 같다.
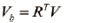(4)
식 (4)에서 회전행렬 R의 역행렬은 전치행렬과 같다. 쿼드로터 시스템의 각속도는 식 (5)와 같다.
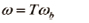(5)
여기서 ωb는 물체 좌표계에서 쿼드로터의 각속도이고, T는 글로벌 좌표계와 물체 좌표계 사이의 각속도 간의 관계를 나타내는 행렬이다. 물체좌표계에 대한 각속도와 오일러각의 회전속도 사이에는 식 (6)과 같은 관계가 성립한다.
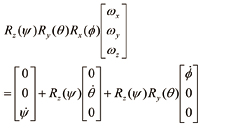(6)
식 (6)에서 RT를 양변에 곱해주고 우측항의 행렬을 계산하면 식 (7)을 유도할 수 있다.
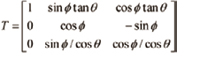(7)
2. 동역학
식 (3)과 (5)를 미분하면, 물체 좌표계에 대한 쿼드로터의 가속도와 각 가속도에 대한 식을 유도할 수 있다.
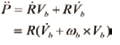(8)
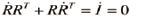(9)
Orthonormal한 회전행렬 R은 RRT=I로 나타낼 수 있는데, 이것을 미분하면 반대칭 행렬 식 (10)을 유도할 수 있다.
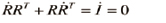(10)
어떠한 고정된 벡터 p'가 회전행렬에 의해 회전된 벡터 p=Rp'를 시간에 대해 미분한 식 (11)과 물체 좌표계에 고정된 벡터 p'가 있고, 글로벌 좌표계를 기준으로 물체 좌표계가 ω로 회전하고 있을 때의 식 (12)를 비교하면 식 (8)을 유도할 수 있다.
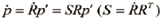(11)
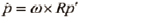(12)
쿼드로터의 병진운동 방정식은 식 (8)을 통해 나타낼 수 있는데, 병진운동에 관한 힘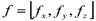 
는 실제로 중력의 영향을 받기 때문에 식 (13)과 같이 나타낼 수 있다.
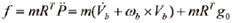(13)
식 (13)을 기체의 가속도에 관한 식으로 나타내면 식 (14)와 같다.
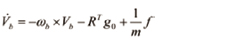(14)
여기서, 
로 중력 가속도를 나타낸다.
병진 운동 방정식과 마찬가지로 뉴턴의 제2법칙인 모멘트 보존법칙을 이용하여 식 (15)와 같이 나타낼 수 있다.
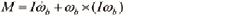(15)
여기서, I는 관성모멘트이다. 쿼드로터 시스템은 선대칭이기 때문에 관성모멘트는 식 (16)과 같다.
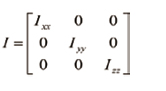(16)
글로벌 좌표계에서 식 (15)에 식 (5)와 (9)를 대입하면 식 (17)과 같다.
(17)
글로벌 좌표에서의 각 가속도에 대한 식을 구하기 위해 식 (17)을 정리하면 식 (18)과 같다.
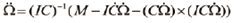(18)
코리올리스와 구심력이 없다고 가정하면, 식 (14)와 (18)은 식 (19)와 식 (21)로 간략화할 수 있다.
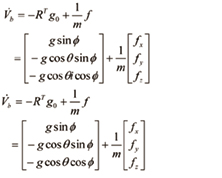(19)
여기서, 기체에 작용하는 힘은 고도와 Roll, Pitch, Yaw 축을 제어하기 위한 추력 
만 존재하기 때문에, 
이다. 글로벌 좌표에 대한 가속도를 구하기 위해서 식 (19)의 양변에 회전행렬 R을 곱해주면 식 (20)을 구할 수 있다.
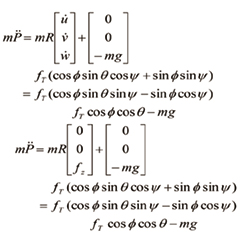(20)
그리고 식 (18)은 식 (21)로 간략화된다.
(21)
식 (21)을 물체 좌표계로 나타내면 식 (22)와 같다.
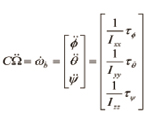(22)
위의 식들을 이용해 최종 동역학을 식으로 나타내면 (23)과 같다[11, 12].
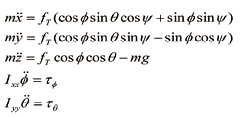(23)
여기서 추력 ft와 각 축에 대한 토크는 다음과 같은 식으로부터 구할 수 있다.
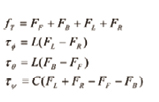(24)
그리고 각 힘들을 간단하게 표현하면 식 (25)로 나타낼 수 있고, 이것을 행렬로 표현하면 식 (26)과 같다.
(25)
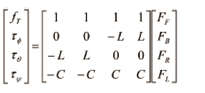(26)
각 rotor에서 발생하는 힘들을 계산하기 위해 식 (25)의 양변에 행렬 C를 곱해주면 제어 입력에 따른 각 rotor의 추력을 나타내는 식 (27)을 구할 수 있다.
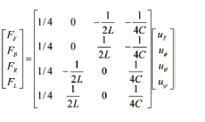(27)
쿼드로터의 자세제어
쿼드로터의 장점인 호버링을 수행하기 위해서는 자세제어가 잘 되어야 한다. 자세제어란 정지비행에 필요한 롤, 피치, 요 각을 제어하는 것을 말한다. 여기서는 롤과 피치 각도를 제어했다. 두 가지 제어방식을 비교해 보자.
1. 각도 검출을 위한 센서 융합
이전 호에서 두 바퀴 구동 이동로봇의 밸런싱 각도를 정확하게 검출하기 위해 자이로와 기울기 센서를 융합한 complementary filter를 사용했다[15]. 쿼드로터의 각도를 정확하게 검출하기 위해서는 자이로 센서와 가속도 센서를 융합한다. 그림 3에 나타난 것처럼 complementary 필터와 Kalman 필터를 사용하여 센서를 융합했다.
그림 3. 각도 검출 블록선도
이 필터에 대한 자세한 내용은 이전 호의 내용을 참고하기 바란다.
2. 선형제어 방식
선형제어에 가장 많이 사용되는 방식은 PID제어 방식이다. 식 (23)에서 보면 전체 동역학식은 비선형이지만 롤, 피치, 요는 관성 시스템의 선형식으로 간단화된 것을 볼 수 있다. 쿼드로터 시스템에서는 PID 제어기 대신에 PD제어기를 사용했다. 그 이유는 각도를 검출하는 센서에 따라 적분기의 경우 각도의 누적오차가 제어 성능에 나쁜 영향을 줄 수 있기 때문이다.
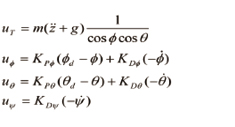(28)
여기서 g는 중력 가속도, z는 고도이고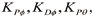 
는 제어기 이득값이다.
3. 시간지연 제어 방식
식 (23)에서 표기된 각도에 대한 동역학 식은 간단하게 표현된 것으로 실제로는 비선형이다. 또한, 가벼운 기체인 쿼드로터 시스템은 외란에 취약한 단점을 가지고 있다. 외부의 방해 요인은 바람이 있고 내부적으로는 모델이 안 된 동역학, 로터의 진동 그리고 기체의 구조 등 다양하다.
이와 같은 외란과 불확실성에 대처하기 위해서 시간지연 제어기를 사용했다. 시간지연 제어기는 이전 토크에서 외란이 포함된 현재 모델을 뺌으로써 외란을 제거하는 일종의 관측기이다. 시간지연 방식은 시간의 차이를 이용하므로 샘플링이 느리면 문제가 될 수 있다. 하지만 최근의 하드웨어는 충분히 빠른 샘플링을 제공할 수 있다.
시간지연 제어기를 구성하는 데 필요한 정보는 시스템의 가속도와 관성이다. 그림 4는 시간지연 제어기의 블록도이다.
그림 4. 시간지연제어기의 블록선도
시간지연 제어기는 각 가속도 값을 사용하기 때문에 잡음에 약한 단점을 가지고 있다. 그러한 문제점을 해결하기 위해 실제 시스템에서는 그림에서와 같이 Q필터를 사용했다.
Q필터는 일반적으로 다항식으로 설계하나, 이 논문에서는 1차 저역통과필터의 간단한 형태로 설계했다[11, 12].
PD제어기만을 사용했을 때에는 불확실성이 남아있어, 정상상태가 되어서도 정확하게 원하는 토크를 얻을 수 없고, 또한 불확실성을 예측할 수 없기 때문에 외란에 취약하다. 하지만 PD제어기에 비해 시간지연 제어기는 식 (3)과 같이 이전 토크에서 현재 모델을 빼줌으로써 불확실성을 예측할 수 있기 때문에 외란에 대해 PD보다 강건하리라는 것을 알 수 있다.
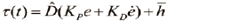(29)
여기서 
은 관성에 대한 평가치이고 불확실성에 대한 평가 -h는 다음과 같이 이전 샘플에서의 토크값과 가속도 정보로 표현된다.
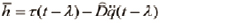(30)
여기서 λ는 샘플링 시간이다. (29)와 (30)을 합하면 전체적인 제어식은 다음과 같다.
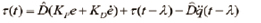(31)
이처럼 시간지연 제어 방식은 제어식이 매우 간단하다. 하지만 그 성능은 가속도 정보의 정확도에 의존하는 것을 알 수 있다.
4. 실험환경
외란에 대한 제어기의 성능을 비교하기 위해 그림 5와 같은 실험환경을 설치했다.
그림 5. 자세제어 실험환경
쿼드로터 시스템은 자유롭게 움직일 수 있는 거치대 위에 놓여 있고 한 축에 무게추를 달아 일부러 시스템의 불균형을 유도했다. 이 무게추를 손으로 들었다 놓기를 반복하며 외란을 주었다.
PD제어기와 시간지연 제어기의 성능을 각각 실험을 통해 비교 평가했다.
5. 실험평가
그림 6은 롤각도에 대한 PD제어기와 시간지연 제어기의 성능을 보여준다.
그림 6. Roll 축의 성능
관성은 실험적으로 구한 값 
=0.036을 사용했다.
그림 6(a)는 PD제어기만을 사용했을 경우의 결과이고 그림 6(b)는 시간지연 제어기를 사용한 결과이다. 시간지연 제어기를 사용한 경우에 오차가 반 이상으로 줄어듦을 볼 수 있어 외란에 대해 더 강건한 것을 확인할 수 있다. 그림 7에 나타난 pitch 각도에 대한 실험결과도 시간지연 제어기의 오차가 반 이상 줄어든 유사한 결과를 보여준다.
그림 7. Pitch축의 성능
6. 실외주행평가
마지막으로 실외에서 주행을 실험했다. 그림 8은 실외주행의 모습을 나타낸다.
그림 8. 실외 비행실험
맺음말
이 글에서는 최근에 많은 연구가 되고 있는 무인비행체의 하나인 쿼드로터 시스템에 대해 살펴보았다. 기구학과 동역학을 유도하고 이를 기반으로 자세제어를 수행했다. 외란의 영향을 많이 받는 쿼드로터 시스템의 성능을 개선하기 위해 비선형 제어기인 시간지연 제어기를 사용했다. 한 축에 무게추를 달아 임의로 외란을 주고 롤과 피치 축의 움직임을 확인해 보았다. 실험을 통해 PD제어기보다 시간지연 제어기의 성능이 우수함을 확인했다.
앞으로 민간용 무인비행체의 사용이 폭발적으로 늘어날 것으로 전망되는 바 쿼드로터 시스템의 제어와 응용에 대한 연구와 발전이 기대된다.
정슬 충남대 메카트로닉스공학과 교수 (jungs@cnu.ac.kr)
