기계공학에서의비선형특성(Ⅰ)
배영철 전남대학교 공과대학 전기공학과 교수(ycbae@chonnam.ac.kr)
이번 호부터는 기계공학에서의 비선형 특성을 다룬다. 주로 기계적 진동에서 어떤 비선형 특성 즉, 카오스적인 거동이 있는지를 살펴본다.
기계공학에서 비선형성의 일반적인 자원 [1]
우리 자신들과 우리 주변의 모든 세상은 본래부터 비선형성이다. 즉 이 세상은 모두 비선형 시스템으로 구성되어 있다고 해도 과언이 아니다. 그러나 많은 경우에 만약 우리가 작은 영향과 변화만을 고려한다면 비선형 시스템을 해석하는데 비선형 방법 이외에 선형 근사 기법을 이용하며, 이 기법은 종종 비선형 거동의 이해, 예측, 제어하는 데 충분하다.
비선형성들과 물리적, 기계적 세계에서 비선형성들의 중요성은 매우 다양화되었으며 비선형성 연구를 위한 이론적 체계와 수학적 체계에 대응하는 연구 개발 방법들은 아직도 유아기이다. 이러한 많은 비선형 특성 중에서 특별히 기계공학에서의 가장 일반적인 자원을 검증하는 몇 개의 예제들을 살펴보고자 한다.
기하학적인 비선형성들
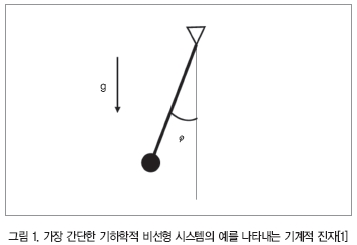
가장 최초이며 가장 간단한 것 중의 하나는 순수 운동학 형태로부터 나오는 기하학적 비선형성이다. 기하학적 비선형의 가장 간단한 예는 그림 1에서 보여주는 것과 같은 진자이며 이는 식(1)과 같이 지배되는 동적 방정식으로 나타낼 수 있다.
평형 Ø=0의 하강점 부근의 가장 적은 발진들에 대하여 이 방정식은 선형화할 수 있지만 우리는 큰 발진과 진자의 회전운동에서 비선형성이 중요하므로 여기에 관심을 둔다.
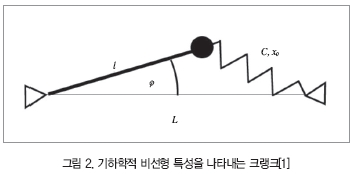
기하학적 비선형 시스템의 다른 사례로는 그림 2와 같이 기계의 모든 종류에서 일반적으로 사용하는 크랭크 기구를 들 수 있다.
이 크랭크는 강성 C를 가진 스프링과 자유 길이 x0를 가진 스프링에 의해 고정된 점에 부착된 회전하는 봉으로 구성한다. 스프링에서 스프링의 편향은 인가된 힘에 비례하고 이것의 진폭에 대응하지 않는다는 조건의 선형으로 가정한다. 그림 2와 같은 시스템의 지배 방정식은 식(2)와 같이 정리된다.
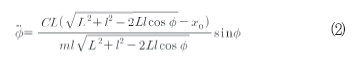
물리적 비선형성들
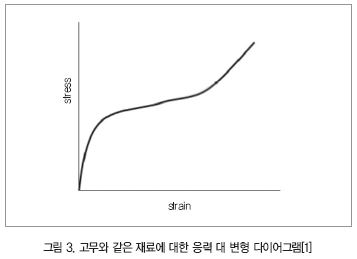
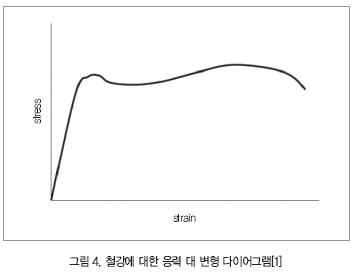
스프링의 선형성과 관계되는 이 가정은 또한 작은 편향에 대하여 오직 정확하다. 그림 3의 고무와 그림 4의 철강 모두는 만약 인가된 부하가 충분하게 크다면 응력과 변형 사이의 비선형 관계를 검증한다.
그림 3과 4에서 보듯이 이들 2개의 다이어그램은 기계공학에서 물리적 또는 재료 비선형성 특성을 보여주는 가장 일반적인 것으로 선형적인 특성을 찾아볼 수 없다.
구조적 또는 설계된 비선형성
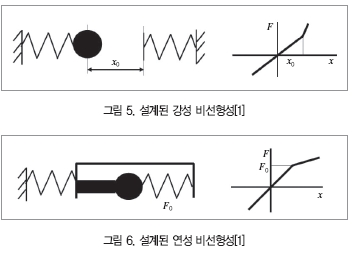
스프링의 비선형 특성은 다양한 응용에서 사용되길 바라고 있다. 이러한 관점에서 설계된 비선형성의 2개의 간단한 예를 그림 5와 그림 6에 나타내었다.
첫 번째 예에서 스프링 시스템의 강성은 변형이 특정의 값 x0을 넘어섬으로써 질량의 오른쪽에 있는 스프링이 능동적으로 동작된 이후에 증가한다. 이 거동은 경성(hardening)이라 불리고 때때로 발전적인 강성 특성으로서 기술된다. 여기에서는 2개의 스프링 사이에 설계된 명확성을 통하여 달성됐다.
두 번째 예제에서 스프링에서 시스템의 강성은 질량의 오른쪽 스프링이 활성화된다. 즉, 외부 힘이 앞선 부하 F0보다 작거나 이후 부하가 특정 값 F0를 넘어섬으로써 감소한다. 이거동을 일반적으로 연성(softening)이라고 부른다.
이들 2개의 예제는 구조적 비선형성들의 그룹에 속하고 어떻게 쉽게 비선형 특성이 선형 성분의 적절한 조합에 의해 설계될 수 있는지를 보여준다.
제한들
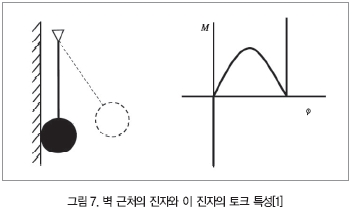
일방적인 제한들은 구조적 비선형성들의 다른 중요한 예이다. 이것은 비선형성의 중요한 자원이며 앞으로 광범위하게 설명하게 될 것이다. 여기에서는 그림 7에서 보여주는 것과 같은 강체 벽 부근에 매달린 진자를 보여주는 오직 하나의 예를 들어 설명한다.
그림 7에서 보여주는 이 시스템은 간단한 비선형이 아니다. 질량과 벽 사이의 충돌을 기술하기 위하여 몇 개의 추가적인 가설들이 필요하다. 이 경우에 우리가 강체 몸체 기구들의 체계에서 머물러 있는 한 최소한으로 이 시스템은 선형화될 수 없다. 오직 한쪽의 운동학적 제한들은 비선형성에서 중요한 자원이다. 뉴톤 방정식들이 좌표와 힘에 대응하여 선형일지라도 계산속으로 명시적으로 제한을 취한 일반화된 좌표들에서 라그랑지Lagrange's) 방정식들은 비선형이다. 예제로서 그림 8과 같은 크랭크 기구를 고려해보자.
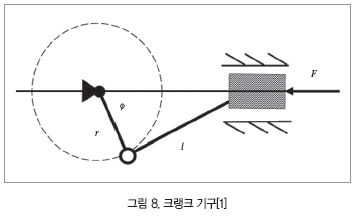
이것의 위치는 크랭크와 수평축 사이의 각도 Ø에 의해 완전하게 특성화될 수 있다. 슬라이더의 위치는 이 각도의 항에서 항상 식(3)과 같이 표현될 수 있다.
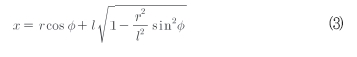
이 관계는 명확하게 비선형이며 기구를 지배하는 라그랑지 방정식을 유도한다.
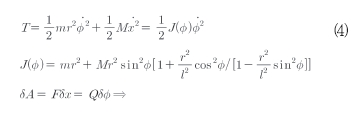
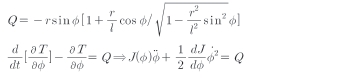
여기서 mr2은 크랭크 관성, M은 슬라이더의 질량, T는 전체 메커니즘의 운동 에너지, Q는 가상 작업에서 관계를 통하여 얻어진 일반화된 힘이다.
식 (4)의 첫 번째 방정식은 완전히 비선형이지만, 우리는 첫 번째 방정식의 왼쪽에 있는 두 번째 항에 관심을 두게 될 것이다. 이것은 ·Ø2에 의존한다. 이것은 식(3)의 운동학적 결합으로 인하여 가변적인 유효관성 J(Ø)이 된다. 일반화된 속도상의 이 비선형 의존성은 다양한 기구에 대해서 일반적이다.
마찰의 비선형성
최근에 비선형성의 자원 중에서 언급하는 것은 제동(damping)이다. 제동 메커니즘들은 극도로 복잡하며 재료들, 그들의 표면들 그리고 박막에서 미세 과정과 깊게 연결되어 있다. 점성 제동의 가장 간단한 모델은 비선형이다. 일반적으로 이들은 식 (5)와 같이 표현된다.
여기서R은 속도에 대하여 직접적인 제동력이다. 함수 f(|ν_|)는 마찰력이 속도의 진폭에 의존한다는 것을 설명한다. 보통의 선형 제동은 f(|ν_|) = b|ν_|에 대응한다. 이 제동은 응용에서 극도로 드문 일이다. 오직 실제 사례는 긴 파이프에서 정상흐름(stationary flow)이다. 그럼에도 만약 실제 제동 기구 가 미지수일 때 선형 제동은 매우 자주 사용됐지만 몇 에너지 소산은 해석을 위해서 필요하다. 더 실제적인 것은 멱급수 f(ν) = b|ν| α, 1⋏α≤2이다. 이것은 높은 레이놀드 수에서 유체 제동을 기술한다. α=2인 경우는 완전히 개발된 공기에서 일반적인 난류 흐름turbulent flow)에 대응한다.
2개 표면 사이의 접촉에서 마찰은 접촉 면적에서 정상적인 힘과 상대적인 속도 모두인 f(V)=μN에 의존한다. 건식 마찰의 1차원인 경우에 식(5)의 관계는 일반적으로 식(6)과 같이 정리된다.
그러나 여기서 마찰계수 μ는 상수가 아니다. 더욱이 공식 관계 식(6)은 함수가 아니다. 이것은 ν=0에서 정의되지 않는다. 이 특별한 경우는 소위 sticking(끈적거림, 달라붙는)이라 불리는 것이 대응하며 일반적으로 분리 계수μs에 의해서 기술되었다. sticking 기간의 마찰력은 식(6)의 방정식에 따라서 계산될 수 없다. 이것은 계산된 값이 최댓값을 넘어서지 못하는 동안 ν=0 조건에 의해 결정된다.
만약 여기서 sticking을 생각한다면 식(7)의 부등식에서 시작하는 미끄러짐은 파괴된다. 가장 간단한 쿨롱의 마찰 법칙( μ=상수)을 그림 9(a)에 보여 준다.
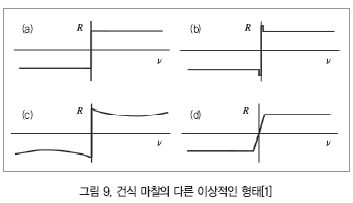
sticking 마찰을 취한 마찰력은 그림 9(b)에 보여준다. 그림 9(c)는 작은 상대 속도들에서 힘-속도의 음의 기울기를 취하는 마찰계수를 보여준다. 이 감소 마찰 계수는 이들 사이의 다양한 마찰 파트너와 유체(공기, 물, 기름)에 대한 수치 실험에서 확인된다. 이것은 sticking의 가능성을 취하지 않으며 sticking이 일어나지 않는 곳에서 오직 적용할 수 있다.
섭동 해석 기본 개념
1. 표준 형태에서의 시스템과 자유 제한에서의 변화
섭동 기법의 주요 개념을 설명하기 위해 비섭동에 근접한 시스템을 고려하자. 이것은 비섭동 시스템의 해를 쉽게 찾는다고 생각하자. 다른 말로 하면 이것은 비섭동 시스템이 폐형(closed form)에서 적분 가능한 것으로 생각할 수 있다. 식(8)과 같은 시스템을 고려하자.
일반 해를 식(9)와 같이 알고 있다고 가정하자.
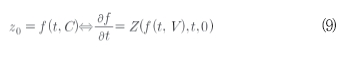
여기서C는 임의의 상수 벡터이며 식(8)의 섭동된 시스템에 대하여 변환으로서 식(9)를 고려하면 식(10)을 얻을 수 있다.
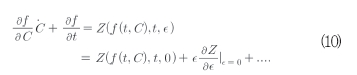
여기서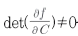 
을 적용하면 식(10)에서 새로운 변수 C를 식(11)과 같이 얻을 수 있다.
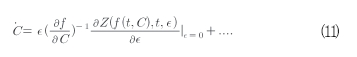
식(11)의 우변 시스템은 작은 파라미터에 의해서 곱해진 평 균법에서 표준형 시스템이라 불리면 일반적으로 식(12)와 같이 표시한다.
여기서 x는 상태 변수들의 n차원 벡터, X는 상태 변수들, 시간과 작은 파라미터ε에 의존하는 n차원 벡터 함수이다.
식(12) 우변 항의 앞부분에 있는 인자가 역시 단순화되어도 작은 파라미터가 남아있으므로 식(12)의 시스템은 표준형이다. 식(12)의 우변 항에서 함수들은 추가적인 경계와 평활을 가져야만 하며 우변 항의 시간 평균은 존재해야만 한다. 이들 추가적인 조건들은 만족하는 것이 언제나 쉬운 일은 아니다. 비섭동 시스템이 식(13)에서와 같이 선형 여기와 제동 발진기일지라도 여기와 제동은 작지 않으며 이것은 표준형으로 직접적으로 변환할 수 없다.
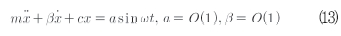
그럼에도 여기에는 섭동 해석이 적절한 2개의 매우 중요한 분류가 존재한다.
첫 번째 분류는 준-보전적 즉, 준-선형 시스템들이 첫 번째 분류에 속한다[2]. 이는 외부에서 인가되는 힘이 없이 반자율적으로 동작한 시스템으로 Duffing 방정식과 Van der Pol 방정식[3]이 시스템의 이 분류에 속한다. 이 이외의 섭동 과 관련하여 준-보전적인 시스템에 대한 많은 다른 예들이 또한 존재한다고 할 수 있다[4-8].
두 번째 분류는 외부의 힘과 관성력으로 지배하는 시스템인 강한 여기를 가진 시스템이다. 이와 같은 시스템의 수치적인 사례[9-10]을 찾을 수 있으며 특별한 문제들을 다룬 경우 도 있다[11-16]. 이 경우의 문제 해결을 위한 지배 방정식은 식(14)와 같이 약간 다르게 쓰인다.
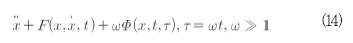
고주파 여기를 포함하는 항 ωΦ(x, t, τ)을 보다 우수하게 포함하는 식(14) 형태는 ω가 큰 파라미터이기 때문에 비자율 시스템을 지배한다. 섭동 동적 시스템의 점근적 해석을 위한 다른 많은 방법이 존재한다. 이들 중 첫 번째는 이 방법들은 그들이 다루고 있는 해의 종류에 따라 다르다. 이들의 많은 방법은 오직 주기 해와 그들의 안정도를 고려한다. 이들 대부분은 포엔카레와 리아프노프에 기초하여 구한다.
동적 시스템의 과도 해를 고려한 다른 방법들은 주기 해 부근의 극한 접근이나 이들의 어트랙션 영역(attraction area)의 해석을 허용한다. 섭동 해석을 위해 현재 가장 많이 사용 하는 3가지 방법에는 표준 평균, 다중 스케일법, 운동의 직접분리 기법이 있다.
2. 표준평균법에 따른 Van Der Pol 방정식에서의 불안정성과 자기 여기 발진
자기 여기를 가진 가장 간단한 방정식을 식(15)와 같이 고려하자.
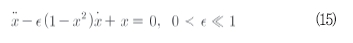
이 시스템에서 제동은 x가 충분히 작은 값에 대하여 음의 값이다. 따라서 평형점 x=0은 불안정하다. x의 더 큰 값에 대하여 1-x2항은 음의 값이며 효과적인 제동은 양의 값을 얻는 다. 이 목적은 불안정한 평형점을 둘러싸는 리미트 사이클을 찾는 것이다.
식(15)에서 비섭동 시스템은 ε=0일 때이며, 이는 식(16)과 같이 정리된다.
이것은 고저파 선형 발진기이다. 이것의 일반해는 식(17)로 나타낼 수 있다.
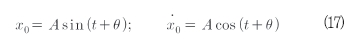
여기서 A, θ들은 자유 적분 상수이다. 이 해는 식(15)의 섭동 방정식에서 변환으로 사용될 수 있으며 식(18)과 같이 정리된다.
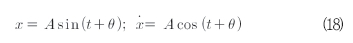
이 변환은 Van Der Pol이라 명명하였고[17] 1926년에 제안되었다. 새로운 변수 A, θ는 식(19)에 의해 지배된다.
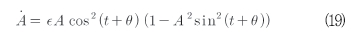
이 시스템은 평균에 대한 표준형을 가진다. 이것은 시간 t에 대응하여 평균처리 될 수 있다. 1차 근사의 방정식들은 식(20)과 같다.
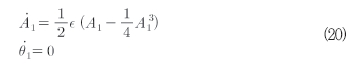
여기서 첨자 1은 1차 근사를 나타낸다. 이들 방정식은 진폭에 대응하여 식(21)과 같이 2개의 정상 해를 가진다.
첫 번째의 하나는 불안정하며 두 번째의 하나는 안정하다. 이것은 원래의 위상 평면에서 안정한 리미트 사이클로 기술된다. 이 경우에 평균 시스템은 완전하게 적분될 수 있다. 이 결과는
상수 t0와 θ0들은 초기 조건들에 의해 결정된다. 원래 변수 들로 되돌아가면 식(23)과 같은 1차 근사를 얻을 수 있다.
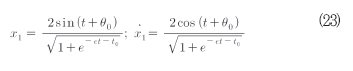
안정한 리미트 사이클은 식(24)와 같다.
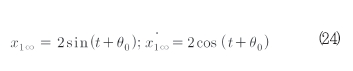
x0〈 2, x0 〉0을 가진 과도 해의 예제는 ε=0.3에 대하여 그림 10에 보여주고 있다.
3. 작은 3차원 비선형성을 가진 시스템에서 주요 공진
식(25)와 같은 작은 3차원 비선형성을 가진 시스템에서 공진 문제를 고려해 보자.
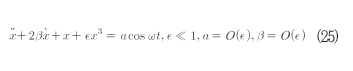
외부 여기의 진폭, 제동, 비선형 항은 작다고 가정한다. 식(25)에 대응하는 비섭동 시스템은 앞의 Van Der Pol의 예제와 동일하다. 따라서 Van Der Pol 변환을 적용할 수 있으며 Van Der Pol과는 약간 다른 형태로 식(26)과 같이 표현할 수 있다.
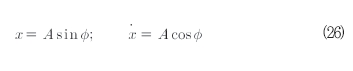
여기서 Ø는 거의 균일한 회전 위상이다. 비섭동 시스템에 대하여 Ø=t+const를 가진다. 새로운 변수들은 식(27)의 방정 식에 의해 지배된다.
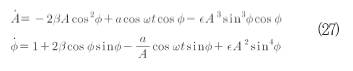
여기서 주요 공진 즉, 외부 여기 주파수 ω는 비섭동 시스템의 자연 주파수에 가까우며 이 경우 거의 주파수가 단일 대역과 같다. 주파수 지연 작은 파라미터로서 동일한 진폭 자수를 가지는 작은 값으로 식(28)과 같이 가정한다.
그런 후 식(27)은 식(29)와 같이 다시 정리할 수 있다.
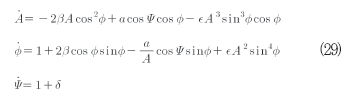
여기서 두 번째 위상 Ψ=ωt을 도입해 왔다. 2개 위상 Ø, Ψ는 거의 동일한 회전 속도를 가진다. 따라서 이것은 이들 사이의 위상차인 식(30)을 소개하는 것이 가능하다.
지금 ψ를 Ψ+θ로 대체하여 식(29)를 다시 쓸 수 있다.
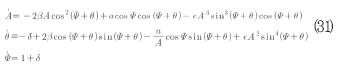
이 시스템은 2개의 저속 변수 A, θ를 포함한다. 고속 위상 Ψ는 독립변수로서 고려될 수 있다. 따라서 이 시스템 식(31)은 표준형을 가지며 이것은 Ψ에 대응하여 평균이 될 수 있다. 1차 근사의 방정식은 식(32)와 같다.
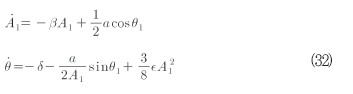
만약 정상 공진 해에 관심을 둔다면 식(32)의 우변 항을 0으로 놓고 식(33)과 같은 진폭을 결정할 수 있다.
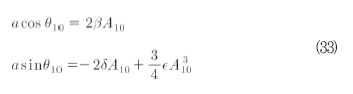
정상 진폭은 식 (34)와 같이 대수방정식에 의해 결정된다.
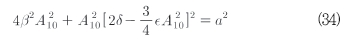
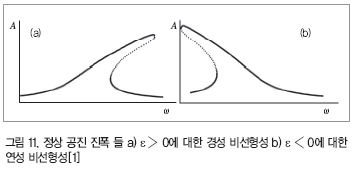
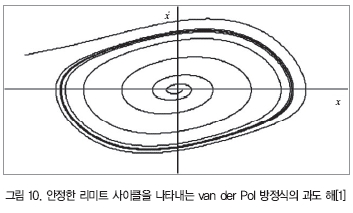
식(34)는 3개까지 양의 해를 가질 수 있다. 이에 대응하는 공진 곡선은 그림 11에 나타내었다. 이들 곡선의 상부와 하부 가지들은 안정하고(실선) 중간 가지들은 언제나 불안정한(점선) 것을 쉽게 볼 수 있다.
비선형 시스템에서 공진 현상을 나타내는 중요한 지시기는 만약 여기 주파수가 증가(또는 감소)라면 정상 진폭들 사이의 차이이다. 예를 들어 경성 비선형성을 고려하자. 만약 여기 주파수를 서서히 증가시킨다면 진폭은 가능한 한 상부의 곡 선이 뒤따른다. 그런 후 이것은 갑자기 뚝 떨어지며 바로 하부 곡선이 뒤따른다. 높은 레벨을 가지고 시작하는 주파수가 감소한다면 상부 곡선으로 뛰어오른다. 따라서 첫 번째 경우의 진폭은 두 번째 경우보다 크다. 만약 우리가 연성 비선형성을 고려한다면 모든 것은 다른 길이 된다.
4. 강한 여기와 3차원 비선형성 시스템에서 2차 공진
ω≈1에서 고려한 공진은 가장 강하지만 이는 3차원 비선형성을 가진 오직 하나의 시스템은 아니다. 여기 진폭이 작지않다고 가정하고 만약 추가적인 공진이 시스템에서 가능한지를 살펴보자. 이를 위해 식(25)와 유사한 식(35)와 같이 표시되는 방정식을 고려하자.
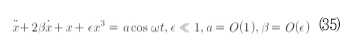
식(35)에 대응하는 비섭동 시스템(ε=0, β=0)은 식(36)과 같이 표시된다.
식(36)의 일반 해는 만약 ω≠1의 더 많은 분석으로부터 주공진을 유도한다면 식(37)과 같이 쉽게 얻어질 수 있다.
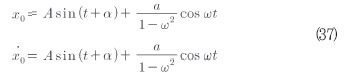
여기서 A, α는 자유 상수들이다. 섭동된 시스템을 조사하기 위하여 식(37)에 기초하여 수정된 Van Der Pol을 적용하면 식(38)과 같이 정리된다.
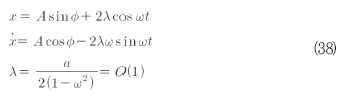
새로운 변수 A, Ø들은 식(39)에 의해 지배된다.
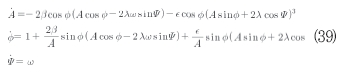
이 시스템에서 무엇이 공진인가? 공진은 우변 항의 시간 평균에서 얻어지는 불연속적인 파라미터의 조합이다. 이 정의 뒤에 숨어 있는 기본적인 개념은 다음과 같다. 2개의 삼각함수 sinω1tsinω2t의 곱을 고려하자. 이것의 시간 평균은 ω1 =ω2의 파라미터 조합을 제외하고 항상 0과 같다. 따라서 이 파라미터 조합은 공진에 대응한다.
식(39) 시스템에 대하여 이 정의가 어떻게 동작하는지를 조사하자. 3개의 방정식은 식(40)과 같은 삼각 식별자를 이용하여 더욱 편리한 형태로 변환될 수 있다.
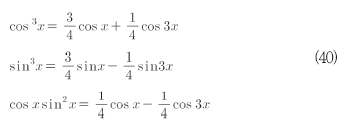
식(40)을 식(39)에 적용하면 식(41)이 얻어진다.
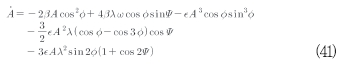
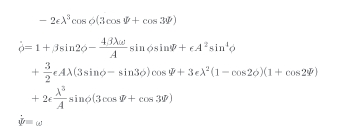
이들 방정식에서의 항들은 불연속 평균을 만들어 낼 수 있는가? 이를 알아보기 위해 t를 통하여 Ø와 ωt을 통하여 Ψ로 대체 할 수 있다. 그러면 이것은 주요 공진은 ω=1의 파라미터 집합에 대응한다는 것이 명확해진다.
이 경우는 앞의 작은 3차원 비선형성을 가진 시스템의 주요 공진에서 이미 설명하였다. 그러나 불연속 항을 만들기 위한 2개의 더 많은 파라미터 집합이 식 (42)와 같이 존재한다.
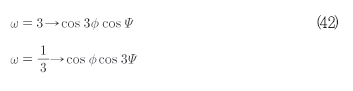
이들 주파수는 이 시스템에서 2차 공진에 대응한다. 첫 번째인 ω=3의 경우를 고려하자. 여기서 선형화된 시스템의 자 연 주파수는 외부 여기 주파수보다 작다. 이에 대한 대응 공진을‘서브하모닉’이라고 부른다.
두 번째인 ω= 1/3인 경우 자연 주파수는 외부 여기 주파수 보다 크다. 이에 대응하는 공진을‘슈퍼하모닉’이라 부른다.
이들 경우에서 정상 진폭에 대한 근사 예측은 작은 3차원 비선형성을 가진 시스템에서 주요 공진의 경우와 유사하게 얻을 수 있다.
참고문헌
1. A. Fidlin, Nonlinear Oscillations in Mechanical Engineering, Springer, 2006.
2. Nagaev R.F. Dynamics of Synchronising Systems. Springer-Verlag, Berlin . eidelberg, 2003.
3. Thomsen J. J. and Tcherniak D. Slow effects of fast harmonic excitation for elastic structures. Nonlinear Dynamics, 17, pp. 227 246, 1998.
4. Bogoliubov N. N. and Mitropolskii Yu. A. Asymptotic methods in the theory of nonlinear oscillations. Gordon and Breach, New York, 1961.
5. Nayfeh A. H. Perturbation methods. Wiley Interscience, New York, 1973.
6. Nayfeh A. H. and Mook D. T. Non-linear oscillation. Wiley, New York, 1978.
7. Van der Pol B. On Relaxation-Oscillations. The London, Edinburgh and Dublin Philosophical Magazine and Journal of science, 2, pp. 978 992, 1926.
8. Sanders J. A. and Verhulst F. Averaging methods in nonlinear dynamical systems. Springer-Verlag, New York, 1985.
9. Blekhman I. I. (Ed) Selected Topics in Vibrational Mechanics. Series on Stability, Vibration and Control of Systems, Series A, Volume 11. World Scientific, New Jersey . London . Singapore . Shanghai . Hong Kong . Taipei .Chennai, 2004.
10. Blekhman I. I., Landa P. S. Conjugate Resonances and Bifurcations of Pendulums under Biharmonical Excitation. In Blekhman I. I. (Ed.) Selected Topics in Vibrational Mechanics, Series on Stability, Vibration and Control of Systems, Series A, Volume
11. World Scientific, New Jersey . London . Singapore . Shanghai . Hong Kong . Taipei . Chennai, pp. 151 . 165, 2004.11. Thomsen J. J. Dynamic Effects of Nonlinearity and Fast Vibrations: Stiffening, Biasing and Smoothening. J. Sound Vibr., Vol. 253 No. 4,pp. 807 831, 2002.
12. Thomsen J. J. Vibrations and Stability. Advanced Theory, Analysis and Tools. 2nd Edition. Springer-Verlag,Berlin - Heidelberg, 2003.
13. Thomsen J. J. Using fast vibrations to quench friction induced oscillations. J. Sound Vibr., Vol.228, No, 5, pp. 1079 1102, 1999.
14. Thomsen J. J. Vibration induces displacement using high-frequency resonators and friction layers. In E. Lavendelis, M. Zakrzhevsky (eds.), Kluwer series: Solid Mechanics and ist Applications, Vol. 37, IUTAM/IFToMM Symposium on Synthesis of Nonlinear Dynamical Systems, August 1998 Riga: Kluwer (Dordrecht), pp. 237 246, 2000.
15. Thomsen J. J. and Tcherniak D. Slow effects of fast harmonic excitation for elastic structures. Nonlinear Dynamics, 17, pp. 227 246, 1988.
16. Thomsen J. J. and Tcherniak D. M. Chelomei's pendulum explained. Proc. of the R. Soc. of London A, 457, 2012, pp. 1889 1913, 2001.
17. Van der Pol B. On Relaxation-Oscillations. The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, 2 , pp. 978 992, 1926.
