[첨단 헬로티]

최근의 인공지능·기계학습 붐에 편승해 지도 분류학습, 회귀학습, 심층학습, 강화학습 등의 ‘메이저’인 기계학습 문제·방법은 널리 알려지게 됐지만, 동적 시스템 학습(learning dynamical systems)이라는 장르는 독자 여러분에게 그다지 익숙하지 않을지도 모른다. 더구나 기계학습의 커뮤니티에서도 동적 시스템 학습이라는 분야가 인지되어 확고한 지위를 구축했다고는 하기 어렵다. 그러나 ‘시스템 동정 문제에 대한 기계학습적인 접근’이라고 표현하면, 동 학회의 여러분들은 대체적인 분위기를 파악할 수 있지 않을까 생각한다.

대부분의 기계학습 입문서에는 ‘데이터 샘플 {x1, x2,..., xn}은 서로 독립 또는 동일한 분포를 따른다(independent and identically distributed; i.i.d.)고 가정한다’라고 밝힌 다음, 지도 학습(분류학습, 회귀학습)이나 비지도 학습(클러스터링, 차원 감소 등)의 설명을 전개한다. 즉 기계학습에서는 샘플끼리 독립인 것이 기본이지만, 그렇지 않은 경우 즉 샘플끼리의 순서관계나 시계열성을 명시적으로 취급하는 것은 약간 특수한 것으로 간주한다.

물론 적용 대상에 따라서는 순서 데이터나 시계열 데이터를 취급하지 않으면 안 되지만, 이러한 경우 우선 고정길이 창을 사용해 벡터화하거나 태스크에 적합한 특징량을 추출함으로써 i.i.d.한 데이터 샘플로 변환, 정적인 시스템을 대상으로 한 기존의 학습 방법을 이용하는 것이 일반적인 기계학습의 ‘작동법’이라고 할 수 있다. 이러한 가운데 시계열 데이터에 특화해, 그 관측 데이터의 배후에 있는 다이내믹스의 생성 모델(generative model)을 추정(학습)하려고 하는 것이 동적 시스템 학습이다. 

그런데 우리 학회지의 독자라면, ‘동적 시스템 학습은 제어학의 시스템 동정과 무엇이 다른가?’하는 의문을 가지는 것이 당연할 것이다. 둘 다 시계열의 계측 데이터에서 동적인 시스템의 모델을 획득하는 것을 목표로 하고 있는 점은 공통적이다. 일반론으로서는 시스템 동정 쪽이 보다 모델을 중시하고 시스템의 제어를 최종적인 목표로 하고 있는 반면, 동적 시스템 학습은 데이터를 중시해 미래 예측이나 이상 검지 등을 목적으로 하는 것이 많다고 할 수 있다.

또한, 시스템 동정에서는 사전에 대상 시스템의 특성이나 이용하는 관측 데이터에 관해 주의 깊게 분석하는 것이 일반적인 데 비해, 동적 시스템 학습에서는 ‘우선 데이터 있음’이라는 입장에서 그 데이터의 생성을 의미 있게 설명할 수 있는 모델을 추정해려는 ‘데이터 드리븐’의 지향성이 강하다. 무엇보다 양자를 목적이나 경향의 차이에 따라 명확하게 구별하는 것은 곤란하며, 앞으로 제어학과 기계학습의 교류가 더욱 깊어지면 방법론·수단도 융합이 도모되어 경계가 점점 더 모호해질 것으로 예상된다. 

이하, 이 글에서는 기계학습의 맥락에서 동적 시스템 학습에 관한 여러 연구를 (1) 최대우도법 접근, (2) 스펙트럼 접근, (3) 뉴럴 네트워크 접근의 3가지로 나누어 해설한다. 또한, 이 3가지의 카테고리는 저자가 이 글을 집필하는데 있어 편의상 이름붙인 것으로, 분야 전체의 동의를 얻은 것은 아니라는 것, 그리고 각 카테고리가 반드시 서로 배타적인 것은 아니라는 것을 밝혀 둔다.

최대우도법에 기초한 동적 시스템 학습 

1. 잠재 변수 모델과 EM 알고리즘 

동적 시스템 학습의 가장 기본적인 방법은 시스템 모델을 확률적인 잠재변수 모델에 의해  표현, 그 모델 파라미터를 최대우도법 등에 의해 추정하는 것이다. 즉, 모델 파라미터를 θ, 계측 데이터를 y1:T, 시스템의 잠재변수(상태변수)열을 x1:T로 했을 때,

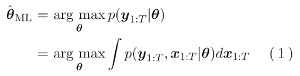
로서 모델 파라미터를 추정한다. 잠재변수 모델(latent variable model; LVM)은 기계학습에서는 클러스터링이나 차원 감소 등의 비지도 학습에서 빈번하게 사용되는데, 상태공간 모델(state space model; SSM)도 잠재변수 모델의 일종으로 해석할 수 있고(그림 1), 잠재변수 모델의 최대우도 추정 방법으로서 대표적인 EM 알고리즘(expectation-maximization algorithm)을 이용할 수 있다.

또한, 모델 파라미터 θ에 대한 사전 분포를 얻을 수 있는 경우에는 최대사후확률(maximum a posteriori; MAP) 추정,

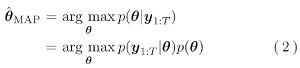
더 나아가서는 점 추정 대신에 파라미터에 대한 사후 분포를 구하는 베이즈 추론(Bayesian estimation)

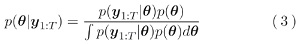
으로 확장하는 것이 가능하다. 또한 이 글에서는 편의 상 MAP 추정, 베이즈 추정에 의한 동적 시스템 학습도 넓은 의미의 최대우도 추정 접근이라고 부르는 것에 주의하기 바란다. 이 접근의 최대 특징은 (1) 모델 파라미터를 고정해 잠재변수(상태 벡터)의 분포를 추정하는 E 스텝과, (2) E 스텝에서 구한 상태변수에 관한 분포에 대한 우도 기대값을 최대화함으로써 모델 파라미터를 갱신하는 M 스텝의 반복에 의해 모델 학습을 하는 점이다. 

2. 선형 상태공간 모델의 EM 알고리즘 

은닉 마르코프 모델(hidden Markov model; HMM)도 잠재변수 모델의 일종으로, 상태공간 모델에 있어 상태변수가 이산적인 값을 취할 경우에 대응하는 것으로 해석할 수 있다. 그리고 HMM을 위한 EM 알고리즘은 1970년대에 이미 바움-웰치 알고리즘으로서 발명되어, 음성인식 등에 응용되고 기계학습 분야에서도 일찍부터 알려져 있었다. 

한편, 의외로 선형 가우스 상태공간 모델을 위한 EM 알고리즘은 1996년에 Ghahramani와 Hinton이 쓴 기술 노트가 최초였으며, 2000년대에 Bishop에 의해 통계적 기계학습의 바이블이라고도 하는 PRML에서 소개됨으로써 기계학습 커뮤니티에 널리 알려지게 됐다. 선형 가우스 시스템의 EM 알고리즘에서는 E 스텝이 Kalman 필터·스무더(Rauch-Tung-Striebel 스무더)에 일치하고 있다.

EM 알고리즘은 언뜻 보면 상호 최소제곱법(ALS)와 큰 차이가 없는 것처럼도 생각되는데, E 스텝에서 각 시각의 상태 xt를 점 추정이 아니라 다차원 가우스 분포로서 구하고, M 스텝에서 우도의 상태에 관한 기대값을 최대화하고 있는 점에서 더 나은 방법이다.

EM 알고리즘에 의한 선형 상태공간 모델의 최대우도 추정은 모델 파라미터 A, C, Q,  에 대해 (공역한) 사전 분포를 도입함으로써 용이하게 최대사후확률(MAP) 추정으로 확장할 수 있다. 또한, 변분 근사나 마르코프 연쇄 몬테카를로법을 이용함으로써 모델 파라미터의 사후 분포를 베이즈 추론하는 것도 가능하다. 또한, 이들 학습법은 비가우스적인 관측 모델을 가진 선형 상태공간 모델의 학습으로도 확장 가능하다. 예를 들면 신경세포의 발화 횟수 천이를 푸아송 분포 선형 상태공간 모델로 모델화해, EM 알고리즘이나 변분 베이즈 EM 알고리즘(VB-EM 알고리즘)으로 모델 파라미터를 학습하고 있다. 

3. 스위칭 동적 시스템의 학습 

선형 상태공간 모델의 확장 방법으로서 복수(유한 개)의 상이한 국소형 모델 간을 확률적으로 천이하는 스위칭 선형 동적 시스템(switching linear dynamical systems; SLDS)가 있다. 이것은 그래프 표현으로 나타내면, 그림 1 (c)와 같이 일반적인 SSM과 같은 연속적인 잠재 상태 벡터 xt와, HMM와 같은 이산적인 값을 취하는 잠재변수 st를 가지는 형태로 되어 있으며, HMM과 SSM의 하이브리드라고도 할 수 있다.

SLDS의 모델 학습에 대해서도 EM 알고리즘에 기초한 최대우도법의 개념을 적용할 수 있다. 즉, E 스텝에서는 모델 파라미터를 고정해 잠재변수인 xt과 st의 동시 분포 p(x1:T, s1:T)을 구하고, M 스텝에서는 구한 잠재변수의 분포에 관한 모델 우도의 기대값을 최대화하면 된다. 그러나 실제로는 K개의 국소 선형 모델을 가지는 SLDS에서는 상태에 관한 필터 분포 p(xt| y1:t)가 Kt개의 컴포넌트를 가지는 혼합 가우스 분포가 되기 때문에 엄밀하게 구하는 것은 곤란하다. 그래서 일반화 의사 베이즈법(generalized pseudo Bayesian; GPB), 가우시안 섬 필터(Gaussian sum filter; GSF), 변분 근사, MCMC 등에 의해 근사적으로 잠재변수 xt과 st의 동시 분포를 구하는 방법이 이용되고 있다.

SLDS는 복수의 동작 모드(레짐)를 천이하는 동적 시스템의 모델화와 인간의 동작·행동 인식 등 응용 범위가 넓지만, 국소 모델의 수를 어떻게 결정해야 할지 하는 문제가 있다. 이것은 일반적인 클러스터링 문제에서 클러스터 수를 결정하는 문제와 비슷하며, 계층적인 디리클레 사전 분포를 이용한 논파라메트릭 베이즈에 의한 모델 수의 결정법 등이 제안되고 있다.

또한, 그림 1로부터도 알 수 있듯이 스위칭 동적 시스템은 보다 복잡한 구조를 가진 잠재변수·상태공간 모델(예를 들면 잠재변수가 복수의 그룹으로 나뉘는 것 등)으로 확장이 가능하다. 실제 이러한 모델은 동적 베이지안 네트워크(dynamic Bayesian networks; DBN)로서 일반화되어, 그 추론·학습법이 연구되고 있다.

4. 비선형·가우스 과정 상태공간 모델의 학습 

최대우도법과 EM 알고리즘에 의한 상태공간 모델의 학습은 상태·관측 모델이 비선형인 경우에도 확장이 용이하다. 즉, E 스텝에서 확장 카르만 스무더(EKS)나 연속 몬테카를로·입자 필터를 이용해 상태 벡터열 x1:T의 사후 분포를 근사적으로 구하고, M 스텝에서는 우도 기대값을 비선형 모델에 포함되는 파라미터에 대해 최대화하면 된다. 이러한 개념에 기초한 초기 예로서는 Ghahramani와 Roweis에 의한 연구를 들 수 있다.

이 연구에서는 상태·관측 모델 모두 방사 기저 함수 네트워크(radial basis function networks; RBFN)가 채용되고, E 스텝에서는 확장 카르만 스무더가 이용되고 있다. 또한, 2000년대에 많은 선형학습 방법이 양정치 커널(positive definite kernel)에 의해 비선형화됐듯이 원래의 공간에서는 비선형인 동적 시스템을 양정치 커널에 의해 무한 차원의 비선형 특징 공간에 사상, 특징 공간에서 EM 알고리즘에 의해 선형 동적 시스템을 학습하는 방법도 제안되고 있다. 

이 밖에도 다양한 비선형 함수 근사기를 상태·관측 모델에 이용하는 것이 가능하지만, 현재는 특히 가우스 과정 회귀(Gaussian process; GP)가 자주 이용되고 있다. 이것은 지도비선형 회귀학습 방법으로서 높은 GP의 성능에 더해, GP가 확률적 모델인 것, 즉 입력을 x, 출력을 y로 했을 때에 조건부 확률 분포 p(y|x)를 자연적으로 구할 수 있는 장점도 갖고 있기 때문이라고 생각된다.

처음에는 잠재 상태열 x1:T를 직접 관측할 수 있다는 강한 가정 하에, 즉 지도 학습의 설정 하에 GP-Bayesfilter나 GP-ADF가 발표됐다. 이들에서는 상태 모델 f와 관측 모델 g의 추정을 각각 지도 회귀학습 문제로서 통상적인 가우스 과정 회귀 문제로 풀고 있다.

그 후, 상태열도 관측으로 추정해야 한다는 지도 학습의 조건 하에서 Wang 등에 의해 가우스 과정 동적 모델(Gaussian process dynamical model; GPDM)이 제안됐다. 이것은 그 전에 정적인 비선형 잠재변수 모델·확률적 비선형 차원 감소법으로서 제안되고 있던 가우스 과정 잠재변수 모델(Gaussian process latent variable model; GPLVM)을 동적 시스템 학습으로 발전시킨 것이다. 단, GPDM에서는 통상적인 가우스 과정 회귀와 마찬가지로 훈련 데이터 샘플을 모두 보존해 둘 필요가 있었다. 그 후 이것을 소수의 가상 샘플에 의해 근사하는 방법이나 변분 근사하는 방법이 제안됐다. 

이와 같이 최대우도법과 EM 알고리즘에 기초한 동적 시스템 학습은, 연속적·이산적인 상태 벡터가 혼재하는 시스템에도 이용할 수 있고, 가우스 과정 회귀와 같은 비선형 모델과도 조합할 수 있다는 점에서 범용성·확장성이 매우 높다. 그 한편 가장 기본적인 선형 상태공간 모델조차 우도함수 즉 목적함수는 다봉성을 가지고 있으며, 적절한 초기 해를 주지 않으면 부적절한 국소 해에 빠져 버리는 문제가 있다. 

스펙트럴 동적 시스템 학습 

1. 시계열 데이터의 차원 감소 

동적 시스템 학습 그 자체는 아니지만, 기계학습·데이터마이닝에서 활발히 연구되어 온 주제의 하나로 (다차원) 시계열 데이터의 변화점·이상 검지 문제가 있다. 이 분야에서는 이데 등이 특이 스펙트럼 해석을 발전시킨 방법을 제안하고 있으며, 널리 알려져 있다. 그 기본적인 개념은 다차원 시계열 데이터에서 고정길이의 슬라이드 창에 의해 부분 시계열을 떼어내 고차원 벡터로 변환, 특이값 분해 혹은 주성분 분석을 적용함으로써 저차원의 부분 공간을 동정한다는 것으로, 확실하게 부분 공간 동정법이나 동적 PCA 등과도 관련되어 있다. 

2. 정준상관분석에 의한 동적 시스템 학습 

제어학에서는 잘 알려져 있듯이 확률 과정의 과거와 미래의 정준상관분석에 의해 상태열을 얻는 방법은 아카이케에 의해 연구되고, 그 후 정준상관분석에 의한 부분 공간 동정법으로서 발전해 왔다. 하지만 의외로 기계학습의 커뮤니티에서는 부분 공간 동정법 자체가 2000년대 후반까지 그다지 알려져 있지 않았다.

비반복적인 알고리즘에 의해 대국 해를 구할 수 있는 부분 공간 동정법은 동적 시스템 학습에 있어서도 매우 매력적이고, 카와하라는 정준상관분석을 이용한 부분 공간 동정법을 양정치 커널에서 정해지는 재생 핵 힐베르트 공간 상에서 전개함으로써 비선형 상태공간 모델을 추정할 수 있는 알고리즘을 도출했다. 또한, 카와하라는 앞의 시계열 변화점 검지 문제에서도, 과거와 미래의 부분 시계열 정준상관분석에 의해 얻은 부분 공간을 이용하는 방법을 제안했다. 그 후 죠우코우 등은 이 개념을 응용해 혼합확률적 정준상관분석(Mixture of Probabilisic CCA; MPCCA)을 이용함으로써 선형 동적 시스템의 확률혼합 모델을 학습하는 방법을 제안했다.

필자가 아는 한, 이들 연구가 부분 공간 동정법을 기계학습의 입장에서 발전시킨 선구적 연구로, 현재 알려져 있는 스펙트럴 동적 시스템 학습의 원조라고 인식하고 있다. 그러나 동적 시스템 학습의 연구자들로부터는 일정한 평가를 받았지만, 기계학습 전체로부터 주목을 받지는 못했다. 

3. 은닉 마르코프 모델의 스펙트럴 학습 

동적 시스템 학습에 있어 스펙트럴 학습이라는 말이 사용되기 시작한 것은, Hsu 등이 은닉 마르코프 모델(HMM)을 위한 비반복적인 알고리즘을 발표한 후부터이다. Hsu 등의 방법은 과거 관측과 미래 관측의 정준상관분석에 의해 이산적인 상태열을 구하는 부분 공간 동정법의 아이디어를 이용하고 있다.

이 방법은 ‘천이 확률 행렬과 관측 확률 행렬의 랭크가 은닉 상태 수와 동일하고, 즉시 출력에서 은닉 상태를 추정하는 것이 가능(1step observability).’하다는 강한 가정 하에 HMM의 학습 알고리즘을 나타낸 것이었는데, 기존 대부분의 기계학습 연구자는 ‘HMM은 EM 알고리즘(Baum-Welch 알고리즘)에 의해 학습하는 것’이라고 믿고 있었으므로 비반복적인 스펙트럴 학습 알고리즘에 의해 대국 해를 얻을 수 있다는 발견은 충분히 충격적이었다. 그 후 많은 연구자들에 의해 전제 조건의 완화와 일반화, 보다 복잡한 모델로 확장이 이루어졌다.

또한, ‘바퀴의 재발명’적인 현상으로도 생각되지만, HMM의 스펙트럴 학습의 성공을 계기로 동적 시스템 학습에서는 연속적인 상태공간 모델의 스펙트럴 학습, 즉 부분 공간 동정법도 다시 주목받는 상태가 되고 있다. 예를 들면 푸아송 분포 출력 모델을 가진 연속적인 상태공간 모델의 스펙트럴 학습을 제안하고 있다.

4. 예측 상태 표현 

기계학습의 주요 분야 중 하나인 강화학습에서는 의사 결정 주체(에이전트)의 이산적 상태 공간 및 천이와 관측을 모델화하기 위해 주로 부분 관측 마르코프 결정 과정(partially observable Markov decision process; POMDP)를 이용하는데, POMDP와는 다른 접근으로서 예측 상태 표현(predictive state representation; PSR)이 있으며, 스펙트럴 동적 시스템 학습 및 부분 공간 동정법과의 관련성이 알려져 있다.

PSR는 HMM의 일반화로서 Jaeger에 의해 제안된 관측 오퍼레이터 모델(observable operator models; OOM)을 Littman과 Singh 등이 더 발전시킨 것으로, 동적 시스템에 대한 입력과 출력에서 시스템의 잠재 상태에 대한 확률 분포 즉 신념(belief)을 양으로 구하는 대신에, 앞으로의 입력에 대한 출력(‘테스트’라고 부른다) 예측의 집합에 의해 시스템 상태를 표현한다는 개념에 기초하고 있다. 특히 Rosencrantz 등은 대량의 테스트 집합을 특이값 분해에 의해 콤팩트한 집합으로 변환하는 변형 예측 상태 표현(transformed PSR; TPSR)를 제안하고 있으며, 선형 동적 시스템에 대한 부분 공간 동정법과의 관련성이 지적되고 있다.

심층 뉴럴 네트워크와 동적 시스템 학습 

1. 뉴럴 네트워크와 동적 시스템 학습 

앞에서 RBFN을 이용한 비선형 상태 공간 모델을 EM 알고리즘에 의해 학습하는 Roweis 등의 연구를 소개했는데, 그 후에는 양정치 커널이나 가우스 과정 회귀를 이용한 비선형화가 주류가 되어, 인공 뉴럴 네트워크와 상태공간 모델을 조합한 동적 시스템 학습법은 다층 퍼셉트론(multilayer perceptron; MLP)를 이용하는 등 소수의 예에 한정되어 있었다. 대규모 뉴럴 네트워크 학습의 어려움 및 잠재 상태 사후 분포 p(x| y) 추정의 어려움이 그 최대의 이유이다. 그러나 2010년대에 들어 심층학습이 우선 지도 학습 문제에서 훌륭한 성과를 달성한 결과, 비지도 학습, 그리고 동적 시스템 학습에 대한 응용도 잇달아 보고되게 됐다.

2. 변분 오토 인코더의 동적 시스템 학습 응용

동적 시스템 학습에도 심층 뉴럴 네트워크가 이용되게 된 큰 계기는 변분 오토 인코더(variational auto-encoder; VAE)의 출현이다. VAE의 본래 목적은 주어진 고차원 관측 데이터 y1, y2, ..., yN에 대해 잠재변수 모델, 즉 p(y)=∫p(y|x)p(x)dx를 심층 뉴럴 네트워크의 높은 표현력을 이용해 학습하는 것이다.

전통적인 기계학습에서는 이런 잠재변수 모델은 베이즈 정리를 이용해 잠재변수 x에 대한 사후 분포를 구하고, 그 분포를 이용해 로그 우도의 기대값을 최대화하는 EM 알고리즘(혹은 그 변종)을 이용하는 것이 정석이었다. 그러나 잠재변수 x로부터 관측변수 y가 생성되는 과정을 복잡한 심층 뉴럴 네트워크로 모델화한 경우, 사후 분포 p(x|y)를 구하는 것은 매우 힘들다. 그래서 VAE에서는 잠재변수 사후 분포 p(x|y)를 별도의 뉴럴 네트워크(인코더 네트워크)에 의해 근사해, 로그 우도의 변분 하계를 오차역전파법과 확률경사법에 의해 최대화함으로써 2개의 네트워크를 동시에 학습하는 것으로 이 문제를 해결하고 있다. 

앞에서 말했듯이 상태공간 모델은 잠재변수 모델에 다이내믹스를 추가한 것이기 때문에 심층 뉴럴 네트워크에 의해 상태 천이․관측 모델을 표현한 상태공간 모델에 대해서도 동일한 기법을 이용하는 것은 자연적인 생각이라고 할 수 있다. Krishnan 등은 이러한 생각에 기초해 비선형 상태공간 모델과 관측열로부터 상태열의 사후 분포를 구하는 ‘추론 네트워크’(inference network)를 동시에 학습하는 구조를 제안했다.

이 방법에서 주목해야 할 것은 추론 네트워크는 이른바 상태 추정기(필터/스무더)이며, 동적 시스템의 생성 모델과 동시에 학습되는 점이다. Karl 등도 이와 매우 비슷한 방법으로 VAE을 확장한 비선형 상태공간 모델을 제안했는데, 잠재 변수열 x1:T 대신에 천이 파라미터열 β1:T를 인코더 네트워크에 의해 추정하고 있다는 점이 다르다. 이외에도 Watter 등은 국소 선형의 상태 천이 모델과 VAE에 의한 비선형 관측 모델을 조합한 상태공간 모델, Fraccaro 등은 시변의 선형 천이 모델과 VAE에 기초한 비선형 관측 모델을 조합한 상태공간 모델을 제안했다.

심층학습을 비선형 상태공간 모델에 조합한 연구는 출현된지 아직 얼만 되지 않았지만, 예를 들면 동영상으로부터 동적 시스템 모델을 학습하고 새로운 동영상 데이터를 생성하는 등 매력적인 응용이 기대된다. 

맺음말

이 글에서는 기계학습 분야의 동적 시스템 학습의 개요와 동향을 3가지 카테고리로 나누어 소개했다. 최근 제어학에서도 기계학습에 대한 관심이 높아지고 있다고 들었다. 또한, 기계학습에서도 동적인 시스템을 양으로 취급할 필요성이 커지고 있으며, 제어학의 여러 가지 방법논이나 기법을 배우는 중요성을 느끼고 있다. 앞으로 두 분야의 교류가 점점 더 활발해지고, 상호의 발전에 기여하기를 바란다.

矢入 健久, 도쿄대학 대학원 공학계연구과